Structural Recursion

Recursion is well-suited for problems that have an intrinsic recursive structure. This also applies directly for many data structures, including linked lists (which we've seen before) and trees (which we introduce today). It will also turn out that for some operations, a recursive approach is natural while an iterative approach requires significant additional work.

Updated Spring 2025

Before we get started, I want to share with all of you some thoughts on recent changes to U of M programs and policies. Below is a brief video from a lecture near the end of the Winter 2025 term. The content is still relevant, and I hope may take a moment to reflect and consider your own values and perspective.

1: Recursion on Linked Lists

1.1 Not Started 1.2 Not Started

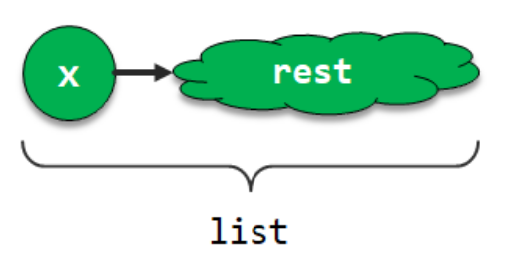
As an initial example, let's consider the recursive structure implicit in a linked list as well as strategies for recursively processing the data stored in the list.

1.1 Exercise: Recursive List Functions

Determine base cases and recurrence relations for the list functions below. Some portions are already given to help you get started. Use the abstract terms in the picture at right, but don't worry too much about precise notation.

This exercise is challenging! Recursion is a totally different kind of thinking than we use in our normal lives. We promise it gets easier. If you get stuck, check the walkthrough video.

length(list)
Finds the number of elements in list.

Base Case	if empty, length(list) = 0
Recurrence Relation	length(list) = 1 + length(rest)

sum(list)
Finds the sum of element values in list.

Base Case
Recurrence Relation

last(list)
Finds the last element in list.
REQUIRES: list is not empty

Base Case	if rest is empty, last(list) = x (Base case is a single element list)
Recurrence Relation

count(list, n)
Finds the number of times n appears in list.

Base Case
Recurrence Relation Hint: Use an if-else here!

max(list)
Finds the largest value in list.
REQUIRES: list is not empty
Hint: Use a helper function max(int,int)

Base Case
Recurrence Relation

You're welcome to check your solution with this walkthrough video.

1.2 Exercise: Coding list_max()

Implement the list_max() function based on the base case and recurrence relation from earlier.

Sample solution…

  // REQUIRES: 'node' must not be null (i.e. the list
  //           starting at 'node' may not be empty)
  // EFFECTS:  Returns the largest element in the list.
  int list_max(Node *node) {
    // (1) base case - hint: take a second look at REQUIRES clause
    if(!node->next) {
      return node->datum;
    }
    // (2) recursive case
    else {
      return max(node->datum, list_max(node->next));
    }
  }

2: Recursion on Trees

2.1 Not Started 2.2 Not Started

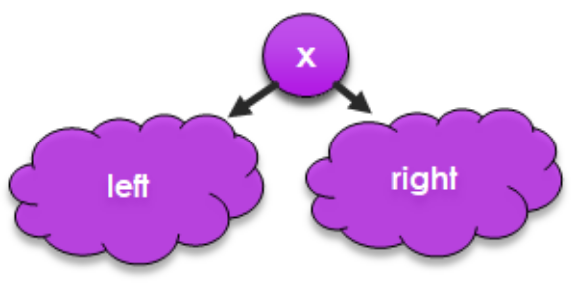
Now, let's take a look at a new data structure, the binary tree. It turns out that binary trees underly many of the most efficient implementations of a variety of data structures, including sets and maps, which we'll talk about next time.

Because trees are also a naturally recursive data structure, we'll apply recursion here as well.

2.1 Exercise: Recursive Tree Functions

Determine base cases and recurrence relations for the tree functions below. Some portions are already given to help you get started. Use the abstract terms in the picture at right, but don't worry too much about precise notation.

This exercise is challenging! Recursion is a totally different kind of thinking than we use in our normal lives. We promise it gets easier. If you get stuck, check the walkthrough video.

size(tree)
Finds the number of elements in tree.

Base Case	if empty, size(tree) = 0
Recurrence Relation	size(tree) = 1 + size(left) + size(right)

height(tree)
Finds the height of tree.
Hint: Use a helper function max(int,int)

Base Case
Recurrence Relation

sum(tree)
Finds the sum of element values in tree.

Base Case
Recurrence Relation

num_leaves(tree)
Finds the number of leaf nodes in tree.

Base Case Hint: there are two base cases here!
Recurrence Relation	num_leaves(tree) = num_leaves(left) + num_leaves(right)

contains(tree, n)
Returns true if tree contains the value n, and false otherwise.

Base Case Hint: there are two base cases here!
Recurrence Relation

You're welcome to check your solution with this walkthrough video.

2.2 Exercise: Coding tree_height()

Implement the tree_height() function based on the base case and recurrence relation from earlier. Note that max() helper function provided.

Sample solution…

  // REQUIRES: 'node' must be a binary search tree
  // EFFECTS: Returns the height of the tree rooted at 'node'.
  int tree_height(Node *node) {
    if(!node) {
      return 0;
    }
    return 1 + max(tree_height(node->left), tree_height(node->right));
  }

3: Tree Traversals

To traverse and process each element in the tree, there are several possible orderings. (Contrast this to a linear data structure like a linked list where there is only one straightforward traversal.)

Let's take a look at each:

Here's a copy of the slide with all the traversals: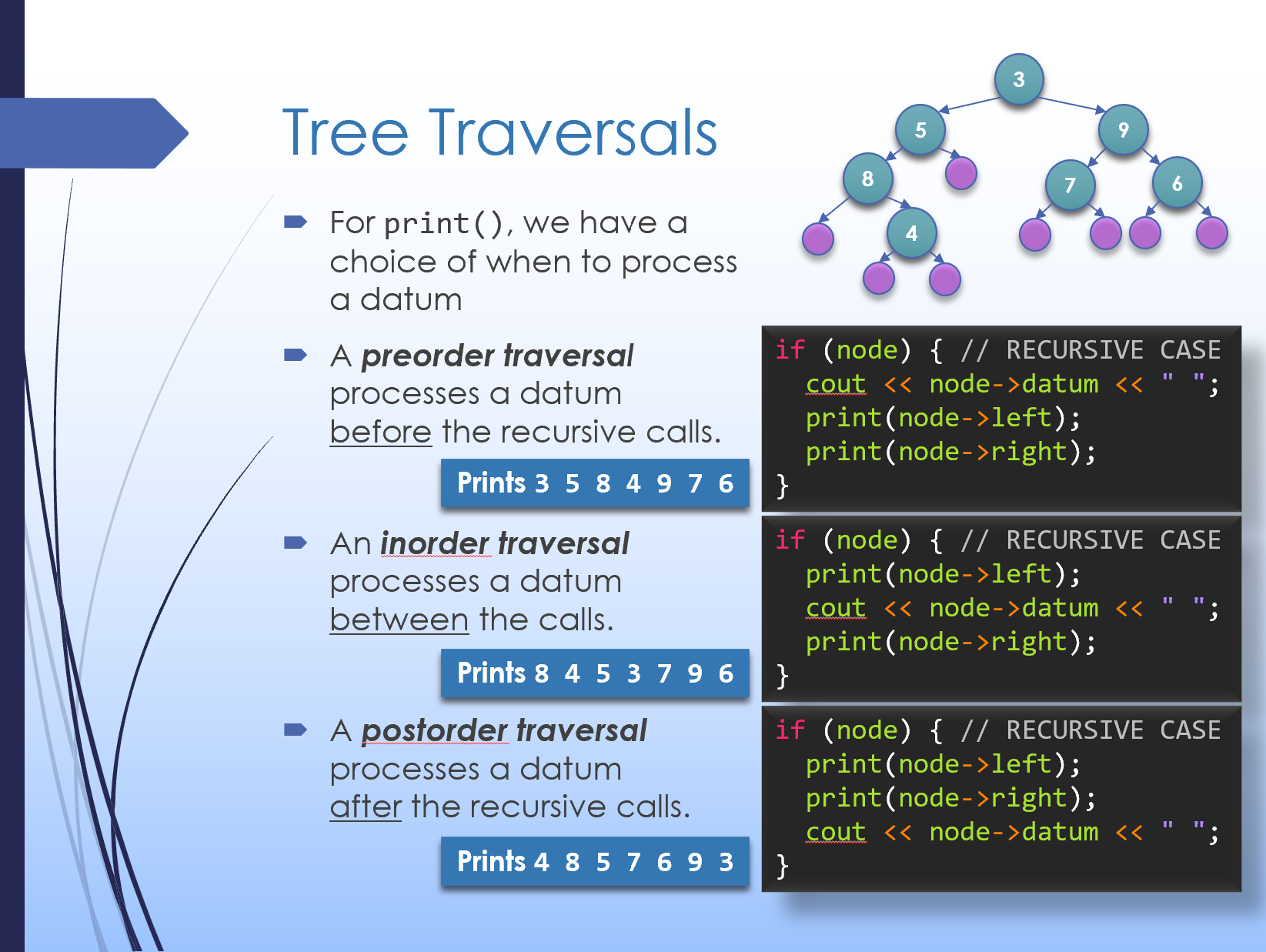

4: Types of Recursion

4.1 Not Started 4.2 Not Started 4.3 Not Started

Finally, let's take a look at several qualitatively different kinds of recursion we've seen so far. Generally, the distinguishing factors are the number and placement of the recursive calls.

4.1

Consider this function. What kind of recursion does it use?

int sum(int n) {
  if (n == 0) {
    return 0;
  }
  return n + sum(n - 1);
}

4.2

Consider this function. What kind of recursion does it use?

void print_list(Node* n) {
  if (!n) {
    return;
  }
  cout << n->datum << endl;
  print_list(n->next);
}

4.3

Consider this function. What kind of recursion does it use?

int fibonacci(int n) {
  if (n <= 1) {
    return n;
  }
  return fibonacci(n - 1) + fibonacci(n - 2);
}

You've reached the end of this lecture! Your work on any exercises will be saved if you re-open this page in the same web browser.

Participation Credit
Make sure to sign in to the page, complete each of the exercises, and double check the participation indicator at the top left of this page to ensure you've earned credit.