Linked Lists
Participation
Loading...

Export your exercise answers to use with another computer or browser.

Linked Lists

Most any data structure uses one of two fundamental approaches in its underlying data representation:

  • Contiguous memory: store elements next to each other in memory (i.e. in an array)
  • Linked structures: store elements separately from each other, connected together via pointers

We've previously covered the contiguous memory approach. In this lecture, we'll begin to explore linked structures. As an initial example, we'll implement a linked list.

1: Sequential Containers and Data Structures

First, let's acknowledge the kinds of sequential containers we'd like to build and the applications they're used for.

2: Arrays vs. Linked Lists
2.1 Not Started

The underlying data structures for these containers must either use contiguous memory or linked structures. Let's take a close look at each approach and compare/contrast the efficiency of several common operations.


2.1 Exercise: Arrays vs. Linked Structures

Describe one of the operations that can be performed more efficiently on an array than on a linked list. Why is this the case and what are the relevant time complexities?

Describe one of the operations that can be performed more efficiently on a linked list than on an array. Why is this the case and what are the relevant time complexities?

There is no walkthrough video for this question, but you can refer back to the video above for examples.

3: Intro to Linked Lists
3.1 Not Started

Here we'll consider building an ADT for a linked Linked List, which is the simplest linked data structure. The key idea is that we implement a sequential container by storing several nodes (each individually allocated in dynamic memory) that contain element values and a pointer to the next node in the sequence. There's no requirement that the nodes are contiguous in memory.

Specifically, we'll start with a "singly-linked, single-ended" list, which we'll call ForwardList (since we can only traverse it in a forward direction).


3.1 Exercise: Linked List Representation Invariants

Here again is the basic data representation for a linked list: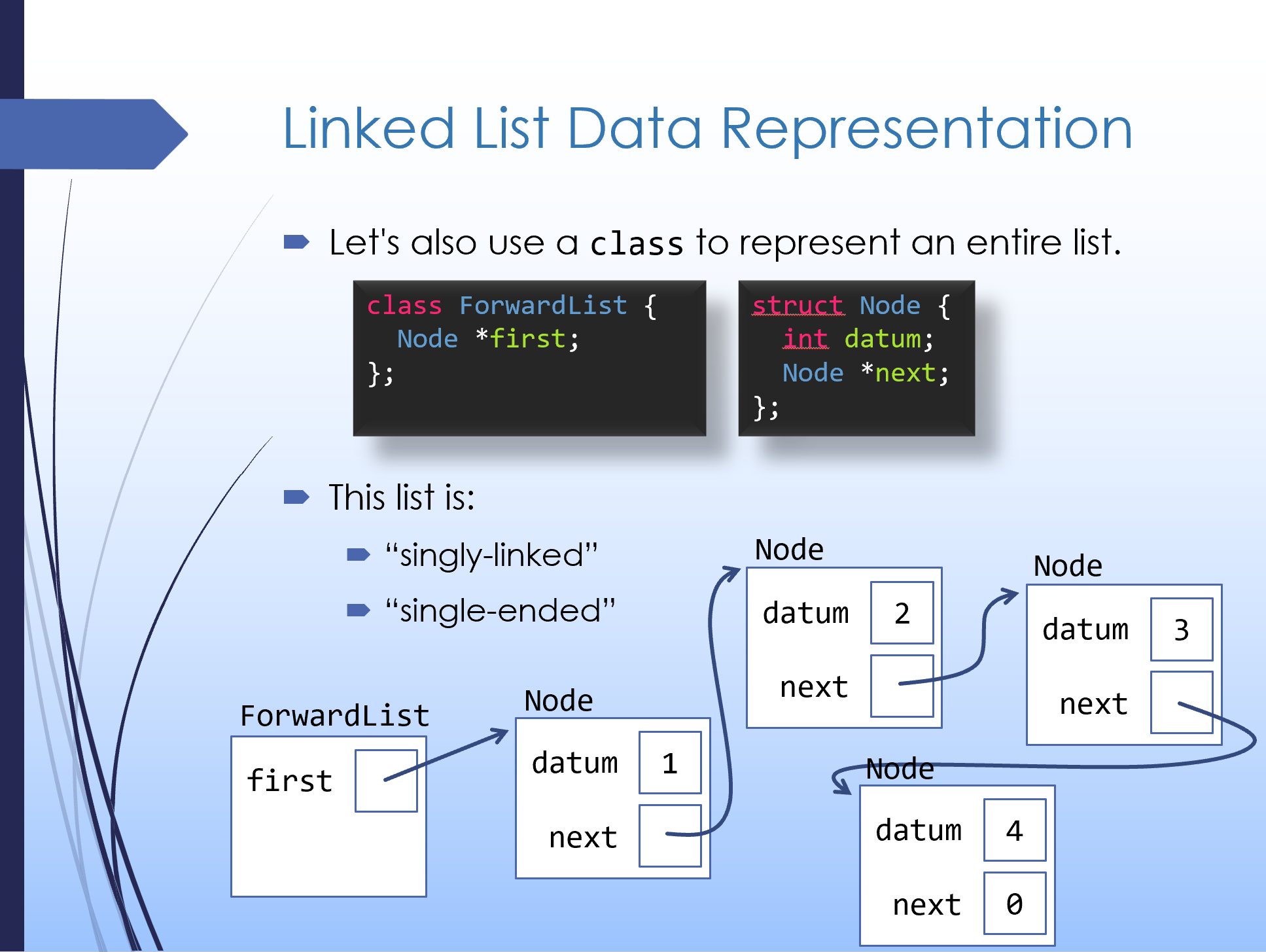


Brainstorm three different representation invariants for the linked list's data representation. Think about what things must be true for the node structure to make sense, or for functions working with the structure to be able to do their job correctly.

Sample solution…

  • first is either null (indicating an empty list) or points to a valid Node.
  • In the last Node, next is always null (i.e. has the value 0x0).
  • For all other Nodes, next points to another Node.
  • A Node may never point to itself. There may be no cycles of next pointers.


4: Linked List Implementation
4.1 Not Started

Let's keep working on the ForwardList class and fill in the implementations of several key functions.


4.1 Exercise: ForwardList::pop_front()

Implement the pop_front() member function for the ForwardList class, which removes the front element from the list. Your implementation should ensure the Node for this element is properly deleted to prevent a memory leak, but you will also need to be careful to avoid undefined behavior! (Hint: For linked list coding, it is VERY helpful to draw a picture.)

Theme: 
template <typename T>
class ForwardList {
private:
  struct Node {
    T datum;
    Node *next;
  };
  Node *first;
public:
  // REQUIRES: the list is not empty
  // EFFECTS:  removes the first element
  void pop_front() {
// This exercise is not automatically graded. // However, getting a correct answer is a bit tricky. // I highly suggest you check the walkthrough video.
  }
};

You're welcome to check your solution with this walkthrough video:

5: Traversing a Linked List
5.1 Not Started

With a data structure based on contiguous memory, walking through increasing indices or addresses is a natural approach. With a linked structure, however, this doesn't work (we can't rely on the contiguous memory assumption anymore). Instead, we have to follow next pointers to traverse from one node to the next.


5.1 Exercise: ForwardList::print()

Implement the print() member function, using traversal via next pointers.

Theme: 
template <typename T>
class ForwardList {
private:
  struct Node {
    T datum;
    Node *next;
  };
  Node *first;

public:
  // MODIFIES: os
  // EFFECTS:  prints the list to os
  void print(ostream &os) const {
// This exercise is not automatically graded. // You can check your solution against the walkthrough video.
  }
};

You're welcome to check your solution with this walkthrough video:



6: Doubly-Linked, Double-Ended Lists
6.1 Not Started

Let's take a look at three upgrades to our data representation and where they make a difference in terms of efficiency:

  • Adding a "previous" pointer to each node in addition to the "next" pointer
  • Adding a "last" pointer to the overall list in addition to the "first" pointer
  • Tracking the current size of the list in a member variable


6.1

Which of the following are true?

7: The Big Three

One more thing - since our class manages dynamically allocated nodes, we'll need custom implementations of "the big three".
You've reached the end of this lecture! Your work on any exercises will be saved if you re-open this page in the same web browser.

Participation Credit
Make sure to sign in to the page, complete each of the exercises, and double check the participation indicator at the top left of this page to ensure you've earned credit.