Array-Based Data Structures
Participation
Loading...

Export your exercise answers to use with another computer or browser.

Array-Based Data Structures

In this lecture and the next, we'll implement a set (an associative container for storing unique elements) based on an array.

We'll be following our normal process for building an ADT - starting with our motivating use cases and the interface we want, followed by a fundamental data representation and invariants, and finally filling in the implementations for each member function.

Updated Fall 2024
1: An Array-Based Unsorted Set

Let's take a look at a data structure to represent an unsorted set. We'll be following our normal process for building an ADT - starting with our motivating use cases and the interface we want, followed by a fundamental data representation and invariants, and finally filling in the implementations for each member function.


Our next step is to choose a data representation and invariants. This ends up as the foundation for the data structure, the implementation of its functions, and the efficiency we can achieve. Throughout the course, we'll end up looking at several different possibilities for an unsorted set. We'll start here with an unsorted array.

2: Implementation
2.1 Not Started 2.2 Not Started

Let's get into the implementation of a default constructor and a few member functions for the array-based unsorted set.


2.1 Exercise: IntSet::insert()

Implement the insert() member function for the IntSet class, which adds a given value v to the set.

First, your code should call contains() as a helper to check if v is already in the set:

  • If the given value is not already in the set, it should add the value to the next available position in the elts array and increase elts_size by 1.
  • If the value is already in the set, insert() does nothing.

The main() function provided includes testing code to verify your implementation. Note that you should not worry about implementing remove() yet… save that for the next exercise below.

You're welcome to check your solution with this walkthrough video:

Note: This walkthrough uses several different files for the code, which is different than the above, where we had everthing embedded into one file. (The solution for insert() is the same, though!)



2.2 Exercise: IntSet::remove()

Below are some potential implementations of the remove() function for IntSet. Which ones work correctly?

It may be helpful to trace through the code on this set, removing the 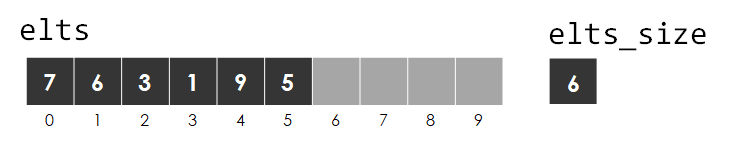1, for example:

Or, you might also consider pasting them into the code for the exercise above and uncommenting the additional set of tests in main() for the remove() function.

Which of the implementations of remove() below are correct? Write "correct" or "incorrect". For each that is not correct, explain what's wrong with it.

// Potential Implementation 1
void remove(int v) {
  int i = indexOf(v);
  if (i == -1) { return; }
  elts[i] = elts[i+1];
  --elts_size;
}

// Potential Implementation 2
void remove(int v) {
  int i = indexOf(v);
  if (i == -1) { return; }
  elts[i] = elts[elts_size-1];
  --elts_size;
}

// Potential Implementation 3
void remove(int v) {
  int i = indexOf(v);
  if (i == -1) { return; }
  elts[i] = elts[0];
  ++elts;
  --elts_size;
}

// Potential Implementation 4
void remove(int v) {
  int i = indexOf(v);
  if (i == -1) { return; }
  for( ; i < elts_size-1 ; ++i) {
    elts[i] = elts[i+1];
  }
  --elts_size;
}

Two of the implementations above for remove() work correctly. Which one is the most efficient for sets with lots of elements? How does this fit in with what the representation invariants require (or rather, what they don't require)?

You're welcome to check your solution with this walkthrough video:


NOTE: For completeness, I'll mention here that ultimately both implementations that work correctly end up having similar runtime complexities in that their runtime scales linearly with the amount of elements in the set - that's because even though the one I describe in the walkthrough video does less work to remove the element, it still needs to call indexOf, which has a linear runtime. We'll talk more about time complexity in the next lecture.

3: Member vs. Non-Member Operator Overloads
3.1 Not Started

You know the only thing cooler than a set ADT? A set ADT with custom operators!

We'll look at two different examples:

  • operator<<, which is implemented as a non-member function operator overload.
  • operator[], which is implemented as a member function operator overload.


3.1 Exercise: Overloading += on IntSet

Let's add a += operator to our IntSet class, which allows a nice syntax for adding elements to the set. Here's an example of how we might use it:

class IntSet {
  // operator+= overload
};
int main() {
  IntSet set;
  set += 3;
  set += 5;
  cout << set; // {3, 5}
}

The += operator can be implemented either as a member function overload or a non-member function overload. Consider each of the potential implementations of += below. For each, indicate how the operator+= overload function is being defined (write "member" or "non-member") and whether or not it is implemented correctly (write "correct" or "incorrect").

// Version 1
void operator+=(IntSet &s, int v) {
  s.insert(v);
}

// Version 2
void IntSet::operator+=(int v) {
  this->insert(v);
}

// Version 3
void IntSet::operator+=(IntSet &s, int v) {
  s.insert(v);
}

// Version 4
void operator+=(IntSet &s, int v) {
  this->insert(v);
}

// Version 5
void IntSet::operator+=(int v) {
  insert(v);
}

You're welcome to check your solution with this walkthrough video:
You've reached the end of this lecture! Your work on any exercises will be saved if you re-open this page in the same web browser.

Participation Credit
Make sure to sign in to the page, complete each of the exercises, and double check the participation indicator at the top left of this page to ensure you've earned credit.